1 Data manipulation and plotting in R

1.1 Introduction

  • Revise the Getting Help section 0.4, and all the Summary subsections (0.3.4, 0.5.5, 0.6.3) from previous chapter.
  • Make sure you downloaded the solution to last week’s coursework and compared it against what you submitted.
  • Create a new R script to save the code you write for this chapter.
  • The purpose of this chapter is to allow you to practice importing, manipulating and exporting data. As well as introduce you to the ggplot2 package, a plotting system for R, based on the grammar of graphics, which tries to make it easy to produce complex multi-layered graphics.

1.2 Working with data in R

R developers have created functions and packages for almost every laborious task that stands between us and good quantitative scientific analysis. Data input, manipulation, and output is easy in R. It is just a matter of breaking down what needs to be done into small achievable tasks, and knowing the right functions.

A data set that has been loaded into R, and is ready for analysis is normally stored by R in something called a data frame. A data frame can be thought of as a table of data where the columns are named vectors, with each vector containing a particular type of data (numeric, string, date, time). These columns are often called variables in statistics. With the rows of the data frame corresponding to individuals or a single observation across the variables.

If, in Chapter 0, the information you collected and calculated regarding gravity at the surfaces of the planets in our Solar System was stored as a data frame it would look like:

Table 1.1: Mass (kg), average radius (m) of each of the planets in our Solar System. Gravity (ms\(^{-2}\)) is calculated at the surface of each planet (distance = 0m).
planet mass radius distance gravity
Mercury \(3.30\times 10^{23}\) \(2.440\times 10^6\) \(0\) \(3.70\)
Venus \(4.87\times 10^{24}\) \(6.052\times 10^6\) \(0\) \(8.87\)
Earth \(5.97\times 10^{24}\) \(6.371\times 10^6\) \(0\) \(9.80\)
Mars \(6.42\times 10^{23}\) \(3.390\times 10^6\) \(0\) \(3.71\)
Jupiter \(1.90\times 10^{27}\) \(6.991\times 10^7\) \(0\) \(24.79\)
Saturn \(5.68\times 10^{26}\) \(5.823\times 10^7\) \(0\) \(10.44\)
Uranus \(8.68\times 10^{25}\) \(2.536\times 10^7\) \(0\) \(8.69\)
Neptune \(1.02\times 10^{26}\) \(2.462\times 10^7\) \(0\) \(11.15\)

To begin building this directly in R, type out the following into a script and run it.

Note that if you have masses and radius already stored in vectors from last week’s script then copy and paste these as appropriate. Reusing your existing vectors from previous chapter to create the planets data frame may look like this:

Check that planet really is a data.frame by typing:

## [1] "data.frame"

In R the class of objects is very important. The same function, for example summary(), will perform differently depending upon the class of the object. In computer programming this is called “function overloading”.

Type planet into the console, and it will display the contents of our newly created data frame. Another way to see the contents, this time in a spreadsheet type view, is to type:

To access the individual variables we use the dollar syntax:

## [1] 3.30e+23 4.87e+24 5.97e+24 6.42e+23 1.90e+27 5.68e+26 8.68e+25 1.02e+26

But we can also use square brackets to select the individual elements of the data frame:

## [1] "Mercury"
##      name    mass  radius
## 1 Mercury 3.3e+23 2440000
## [1] "Mercury" "Venus"   "Earth"   "Mars"    "Jupiter" "Saturn"  "Uranus" 
## [8] "Neptune"
##      name     mass  radius
## 1 Mercury 3.30e+23 2440000
## 2   Venus 4.87e+24 6052000
## 3   Earth 5.97e+24 6371000

Absolute referencing like this is a bad idea. If the order of your columns change, you may be referring to different columns than you thought you where, likewise for rows. By using the dollar syntax, we are using the name of the column, rather than its location in the data frame. Plus it is easier to understand what is happening when you reread the code, as you will see.

If we wanted to calculate the volume of each planet, assuming planets are perfect spheres, we could use the equation for volume: \[ V = \frac{4}{3} \pi r^3, \] where \(r\) is the planet radius:

## [1] 6.084965e+19 9.285074e+20 1.083207e+21 1.631878e+20 1.431220e+24
## [6] 8.270447e+23 6.831819e+22 6.251047e+22

Since we created this data frame, we already know the names of the variable that are contained within it. But say we load a foreign data set, how do we know what the variables are called? Outside R, we hope that this data set also has good documentation, such as a PDF or website telling you all the details you could ever want know. But within R, we can get a list of the attributes of an object by using the names() function:

## [1] "name"   "mass"   "radius"

As well as using names(), it is also good practice to check the size of the data frame.

We previously used length() to determine how many elements were in a vector. Since, a data frame is two-dimensional, we instead use nrow() and ncol() to determine the number of rows and columns respectively:

## [1] 8
## [1] 3
## [1] 8 3

Using the dollar syntax we can create new variables:

Though there are more elegant ways of creating new variables, as you will see in the next section.

1.2.1 Basic manipulation

The easiest way to add distance, and gravity as variables to our data frame is to make use of the dplyr package. Before we can load this package from the R library, you will need to install it:

You only need to install a package once. But you have to load all the packages you want to use at the start of every session. For this reason, make sure all library(...) commands sit at the top of your script. Add library(dplyr) to yours now and run it. Loading the dplyr package gives us access to four functions:

  • filter() Focus on a subset of the rows of a data frame.
  • arrange() Reorders the rows in the data frame.
  • select() Allows you to zoom in on a useful number of columns.
  • mutate() Easily add new columns that are functions of existing ones.

The first argument to each of these functions is always the data frame we wish to work on, the subsequent arguments are the variables we wish to work with. For example, to focus on big planets i.e. those that have radius greater than \(10^7\)m we use the filter() function:

##      name     mass   radius contains_humans radius_km
## 1 Jupiter 1.90e+27 69910000               0     69910
## 2  Saturn 5.68e+26 58230000               0     58230
## 3  Uranus 8.68e+25 25360000               0     25360
## 4 Neptune 1.02e+26 24620000               0     24620

To arrange the planets by increasing size, we using the arrange() function:

##      name     mass   radius contains_humans radius_km
## 1 Mercury 3.30e+23  2440000               0      2440
## 2    Mars 6.42e+23  3390000               0      3390
## 3   Venus 4.87e+24  6052000               0      6052
## 4   Earth 5.97e+24  6371000               1      6371
## 5 Neptune 1.02e+26 24620000               0     24620
## 6  Uranus 8.68e+25 25360000               0     25360
## 7  Saturn 5.68e+26 58230000               0     58230
## 8 Jupiter 1.90e+27 69910000               0     69910
##      name     mass   radius contains_humans radius_km
## 1 Jupiter 1.90e+27 69910000               0     69910
## 2  Saturn 5.68e+26 58230000               0     58230
## 3  Uranus 8.68e+25 25360000               0     25360
## 4 Neptune 1.02e+26 24620000               0     24620
## 5   Earth 5.97e+24  6371000               1      6371
## 6   Venus 4.87e+24  6052000               0      6052
## 7    Mars 6.42e+23  3390000               0      3390
## 8 Mercury 3.30e+23  2440000               0      2440

If we want to store the data in this newly rearranged form then:

If we wanted to remove the column of planet names, effectively anonymising them, we would use the select() function to specify the columns we do want to keep.

In order to carry on with our gravity calculations, we need to add a distance column, use mutate() to do this. Using mutate() we can actually add the distance and gravity variables in one call:

When passing variable names to cal_gravity(), mutate() will check if these names correspond to variables inside the specified data frame. This means we do not have to repeatedly use the dollar syntax mentioned earlier to access the needed variables. Which makes our code look clean and easy to read (providing you know how mutate works).

If there were no variables inside the data frame matching these names, mutate() would then search the local environment. Finally, stating an error if it could not find any object matching the name specified.

Check what the data contained with planet now looks like. Next, arrange the rows by increasing gravity. Where does Earth rank among the Solar System? Are there any other planets were we would either (a) not be crushed to death, nor (b) float off into space if we fell over?

1.2.2 Matrices

To take a bit of a side-step, I just want to explain a bit about matrices in R because they are similar to data frames but with a few restrictions. Though we will not be making use of matrices in this module, you will in the more-theoretical statistics modules.

The word matrix is a mathematical term for a two-dimensional array of numbers, with a vector being a one-dimensional array. To create a matrix we can simply bind vectors together as columns:

##      x  y  z
## [1,] 1  6 11
## [2,] 2  7 12
## [3,] 3  8 13
## [4,] 4  9 14
## [5,] 5 10 15

Or we can create one directly, using the matrix() function:

##      [,1] [,2] [,3]
## [1,]    1    2    3
## [2,]    4    5    6
## [3,]    7    8    9
## [4,]   10   11   12
## [5,]   13   14   15

You can only access the data within a matrix using the square bracket notation. And, all the data in the matrix has to be of the same type. As a result of these restrictions you would not use a matrix to store data as information, but instead you would use matrices to perform algebraic calculations, such as matrix multiplication, or calculating the determinant of a matrix.

1.2.3 Exporting data

Much like when we create custom functions, data frames only exist in our local environment. Which, again, means that when we quit R they will disappear. A good way to export a data frame is to write it as a CSV file to your H: drive. CSV stands for Comma Separated Values, and any self-respecting data analysis software will be able to read a CSV file. To write to a data frame to CSV from R, we make use of the write.csv() function specifying the full file path including the file name and extension:

To see why we use the argument row.names=FALSE, set it to TRUE, rerun the command, and see if you can spot the difference in the file.

Where are these row names coming from? Type row.names(planet) into the console. Row names should just be the equivalent of row indexes i.e. nothing of actual value. Therefore they do not need storing.

This will write a CSV file to the path you have specified. Locate the file, right click and choose to open with a text editor, such as Notepad++. The way the data is laid out in the file should follow the same structure as it appeared in the data frame, but the efficient formatting makes it difficult to read with your human eyes. One thing is clear though, and that is the first row contains the variable names, with the data existing in the remaining rows. If you double-click the CSV file, Excel will probably try to open it, you should try this. Excel is smart enough that will have automatically recognised the format of the CSV file.

Other general data file formats exist, these involve separating values using different methods (tabs or whitespace), see Table 1.2. To work out how to use these write functions and discover how they write your data to a file, check their respective help pages, and open up the resulting file with a text editor, like you did with the CSVs.

Table 1.2: General formats and functions for importing and exporting data.
Name Extension Write function Read function
CSV .csv write.csv() read.csv()
Tab-delimited .tab write.table() read.table()
Fixed Width Format .fwf read.fwf()

The base R packages do not have a write function for FWF, this is because the other two methods are considered sufficient.

1.2.4 Importing data

As you can see, while we have write.*() functions we also have equal and opposite read.*() functions. Try importing the planet.csv file that you produced:

Take a look inside dat, if it looks the same as your planet data frame, then good job!

In general, before you import a data set, try to inspect the file using a text editor to confirm the structure. Once you have identified the structure, and if it happens to be something standard, like a CSV, or tab-delimited file, then go ahead and use those respective functions to read it in. But in the event of it being something a bit more special, like colon separated values, you can setup read.table() to import the data correctly. The read.table() function is considered the Swiss Army knife of the read.*() family6. To see all of the possible arguments for read.table() check its help page.

1.2.5 Using a working directory

Previously, when importing and exporting data sets, we said we had to specify a complete file path such as:

However, R has something called a working directory. If set, anything we save, such as data sets and plots, will be saved to this location7.

Now, of course, if we specify absolute paths, like the one above then we are effectively overriding this feature.

To get the path of your current working directory type into the :

You can change this, by setting it to a different directory using using setwd(), for example:

If I were to run the following command, the filename is now considered relative, i.e. it does not tell R exactly where to save the data. In this case, R assumes it should use the working directory.

So, by setting the working directory at the start of a script, we make our importing-and-exporting lives easier, because we do not have to verbosely state where we want to save something every single time. Also, if future you ever needs to open a script to see where it is saving everything, then this will be obvious from the setwd() near the top of the script.

A relative file path can include folders:

This assumes that there is folder called “data” in my working directory. R will complain if it does not exist.

One final thing about why it is good to use relative paths and “working directories” is that it makes your code more portable. By using relative references, you can bundle your code and data together, allowing someone else to run and modify it on their own system.

It is worth noting that when writing an Rmarkdown file (.Rmd) RStudio assumes that the working directory is the directory that the .Rmd file is saved in.

1.2.6 Summary

  • Data frames are the standard object for storing data in R. Each column in a data frame is considered to be a variable, such that the type of data it contains (strings vs numbers) can differ from the other columns. Accessing data can be done using both the dollar syntax and the square-bracket syntax:
## [1] "Jupiter" "Saturn"  "Uranus"  "Neptune" "Earth"   "Venus"   "Mars"   
## [8] "Mercury"
## [1] "Jupiter" "Saturn"
## [1] "Jupiter" "Saturn"  "Uranus"  "Neptune" "Earth"   "Venus"   "Mars"   
## [8] "Mercury"
## [1] "Jupiter" "Saturn"
  • To manipulate data on a much larger and general scale, it is more efficient to use the functions provided by the dplyr package, namely:
Function Action
filter() Focus on a subset of the rows of a data frame
arrange() Reorders the rows in the data frame
select() Allows you to zoom in on a useful number of columns
mutate() Add new columns that are functions of existing ones

The first argument to each of these functions is always the data frame we wish to work on. With the subsequent arguments involving the names of the variables we wish to operate on or with.

  • To export data use either the write.table() or write.csv() functions. Make sure to set the parameter row.names=FALSE. Check the help pages for each for more details.

  • Both have these have sister functions; read.table() and read.csv(). With read.table() having lots of options that can be modified to read in any structured data file.

  • R has a working directory, use getwd() to find out what it currently is. And use setwd() to change it. Equally, there is a menu in RStudio that allows you to do the same thing.

  • Working directories are good, as they allow you to use relative paths, rather than absolute ones.

  • It can be a good idea to set your working directory at the top of your script.

1.2.7 Exercises

Now complete the following exercises:

  1. Working on your planet data frame:
  1. Add the volumes for each planet as new variable using the dollar syntax.
  2. Using mutate() add variables with the following definitions:
* `mass_earths` The mass of a planet as a proportion of the mass of Earth.
* `volume_earths` Express `volume` as a proportion of Earth's volume.
* `gravity_earths` Express `gravity` as a proportion of Earth's gravity.
  1. Create a new data frame which only contains the names of the planets, and each of the measurements expressed as a proportion of Earth.8 Inspect this data frame for information on the other planets relative to Earth.
  1. Make sure you are familiar with writing and reading from data files that are Tab-delimitted or CSV. For each file format:
  1. Look-up the help page, see the arguments needed to use the particular write.*() function.
  2. Store the planet data frame with the appropriate file extension.
  3. Can you open it in Excel?
  4. Can you read it back into R?

1.3 Data Types

To determine the data type of an object use the class() function. Type in the :

## [1] "numeric"
## [1] "character"
## [1] "character"
## [1] "logical"

Notice how the names of the planets are classed as a factor whereas the vector of strings (peanut and seed) is classed as a character? We will discuss this soon.

More generally, class() can be applied to any object:

## [1] "data.frame"
## [1] "function"

When you start getting a lot of errors, class() can be used to sanity-check your objects; ``Is planet actually a data frame?’’

1.3.1 Numeric

Decimal values are stored as numeric data in R. And it is the default computational data type. If we assign a decimal value to a variable x as follows, x will be of type numeric:

## [1] "numeric"

Furthermore, even if we assign a vector of integers to a variable k, R will still store it as numeric:

## [1] "numeric"

1.3.2 Factors

It is common in statistical data to have categorical variables, indicating some subdivision of the data, such as social class, primary diagnosis, tumour stage, gender, species, etc. Such variables are stored in data files often as strings indicating their actual value, though abbreviations may be used; “m” for male, and “f” for female. But, due to the actual number of observations, it may be more sensible to store the categorical data using numerical codes; 1 for male, 2 for female. With their meaningful names then being store in the documentation for the data.

Regardless of how they are originally stored, in R they should be converted to factors. A factor is a data structure which stores the categorical data as numerical codes, and the labels which make the codes meaningful. For example, say we have a pain variable that records what level of pain our patients are in using a four-point scale:

## [1] none   mild   severe medium medium mild   mild   severe
## Levels: none mild medium severe
## [1] "none"   "mild"   "severe" "medium" "medium" "mild"   "mild"   "severe"

This factor data structure is so routinely used by data scientists that R will automatically convert strings to factors when creating a data frame which includes using any of the read.*() functions. Hence why, even though we originally specified the planet names as a vector of strings, it is now being stored as a factor in R.

After the factor has been created, we can modify its levels, either all at once or individually:

## [1] "none"   "mild"   "medium" "severe"
## [1] "none"          "uncomfortable" "unpleasant"    "agonising"
## [1] "absent"        "uncomfortable" "unpleasant"    "agonising"

1.3.3 Data and time

A date or timestamp typically looks like: 2014-10-09 01:45:00

This follows the format of YYYY-MM-DD hh:mm:ss. But there are a number of other ways of laying out the same information; Americans like to switch the month and day around; the time-part may occur before the date part; we may not have seconds; we may use a letter abbreviation for month. The lack of consistency of how people write timestamps can make them a headache to deal with, especially when we are merging data from two different sources.

By default, R will make no attempt to parse a date or timestamp as such. Instead R will silently read them as strings, and thus will be turned into a factor. This is not useful, and we will cover how to override this behaviour using the lubridate package in Chapter 4, where we deal with parsing differently formatted timestamps, and the tedious issue of time zones.

1.3.4 Exercises

  1. Mercury, Venus, Earth and Mars are called the terrestrial planets, as they are primarily composed of rock and metal. Jupiter and Saturn, are composed mainly of hydrogen and helium, thus are referred to as gas giants. Finally, Uranus and Neptune, are composed largely of substances with relatively high melting points, thus are often referred to separately as ice giants.

Create a factor variable, called type, in the planet data frame with these categories. Make sure the each planet has the correct label.

  1. Convert the contains_humans variable inside planet to a factor with 0 labelled as "no", and 1 as "yes".

  2. See what happens when you convert a factor back to numeric using the as.numeric() function, and how it differs from as.character().

1.4 Logical comparisons and Boolean operations

We have seen that setting up scientific information in the form of one or more vectors is often convenient for performing additional calculations as well as plotting. R is designed around the idea and use of vectors. Data frames are essentially a collection of vectors, but with a bit of extra useful functionality. Furthermore we have seen that R comes with tools for extracting and manipulating the information in vectors and data frames.

In practice, we often have to extract data that satisfy a certain criteria, such as all the data for females, or all those with a particular disease. This is when we start to make statements involving logical comparisons.

1.4.1 Logical comparisons

We have previously seen, that we can select parts of a vector using indexing:

## [1] "Saturn"  "Uranus"  "Neptune" "Earth"

But if we want to specifically look at particular type of planet, then without having to calculate the specific numerical index we can use filter:

##      name     mass  radius contains_humans radius_km distance  gravity
## 1    Mars 6.42e+23 3390000               0      3390        0 3.727724
## 2 Mercury 3.30e+23 2440000               0      2440        0 3.698643
##        type
## 1 ice giant
## 2 ice giant

Where == means “equal to”, see Table for other operators. In fact, you can practically read that last line of code as a sentence; “Filter the rows in the planet data frame such that the type is equal to ice giant”.

Table 1.3: A list of the logical comparison operations available in R.
Symbol Comparison
< Less than
> Greater than
<= Less than or equal to
>= Greater than or equal to
== Equal to
!= Not equal to

Note that when you see a logical comparisons, such as type == "ice giant", R is actually returning a vector of TRUEs and FALSEs:

## [1] FALSE FALSE FALSE FALSE FALSE FALSE  TRUE  TRUE

This is then being used to filter the data frame, returning only the rows that correspond to TRUE.

1.4.2 Boolean operations

The real fun begins when you start combining logical comparisons with Boolean operations. If you are adept at searching the Internet i.e. your Google-Fu is strong, then you will likely be familiar with the phrases; “and”, “or”, and “not”. In R, these words are represented by the symbols is shown below.

Table 1.4: A list of the Boolean operators available in R.
Symbol Phrase
& And (ampersand)
| Or (vertical bar)
! Not or negation (exclamation)

The operators & and | connect two logical comparisons and return TRUE or FALSE depending on the joint truth or falsehood of the two logical comparisons. We also use brackets to help visually separate out the different conditions.

##    name     mass  radius contains_humans radius_km distance  gravity      type
## 1 Earth 5.97e+24 6371000               1      6371        0 9.814479 gas giant
## 2 Venus 4.87e+24 6052000               0      6052        0 8.872362 gas giant
##      name     mass   radius contains_humans radius_km distance   gravity
## 1 Jupiter 1.90e+27 69910000               0     69910        0 25.940784
## 2  Saturn 5.68e+26 58230000               0     58230        0 11.177968
## 3  Uranus 8.68e+25 25360000               0     25360        0  9.005946
## 4 Neptune 1.02e+26 24620000               0     24620        0 11.228770
## 5   Earth 5.97e+24  6371000               1      6371        0  9.814479
## 6   Venus 4.87e+24  6052000               0      6052        0  8.872362
## 7    Mars 6.42e+23  3390000               0      3390        0  3.727724
## 8 Mercury 3.30e+23  2440000               0      2440        0  3.698643
##          type
## 1 terrestrial
## 2 terrestrial
## 3 terrestrial
## 4 terrestrial
## 5   gas giant
## 6   gas giant
## 7   ice giant
## 8   ice giant

The & returns TRUE only when both of the comparisons are true. While | returns TRUE if at least one of the comparisons is true.

1.5 Plots

It might seem to you that scientists have an obsession with quantification. Your impressions would be correct. To build reliable, reproducible results, scientists naturally seek to gather and record counts, measurements, and attributes of the phenomenon under observation. Data, the collective name for such counts, measurements, and attributes, are the lifeblood of science. Studying data with quantitative tools allows scientists to detect patterns, make predictions, and assess the reliability of current theory. Being able to visualise data is crucial to this endeavour. Even a small data set is practically incomprehensible all by itself. Plotting data allows us to visualise the relationships we are interested in.

Visualisation can be used for two things; (a) for the computer to show the scientist what is happening in the data, and (b) for you to show other people. Graphs that fall into (a) tend to be produced quicker and dirtier than the graphs we produce for (b).

Finally, different types of graphs emphasise different aspects of the data and variables under study. Building a good graph therefore takes time and is often an iterative process.

1.5.1 Getting started

Before we begin, you should start a new R script, call it something like chp-1-plots.R.

One more thing is that within RStudio you need to install a package:

If you are on a computer system where you need to install additional packages in a specific folder you can use the lib="filepath" argument.

Once it has installed add library(ggplot2) to the top your new script. This loads the package into your current R session.

You can see all the packages you have loaded in your session using:

Note, if you want to remove a package from your session type (do not do this now):

Also, if when you load in a package and it has a function with the same name as another package that is already loaded in your R session. You will get a warning that one of the function names masks the function from the other package. In such situations, you ensure to use the function from the specific package by prefixing the function name by packagename::, i.e. base::print() ensures you use print() from the base package.

The ggplot2 package is a plotting system for R, based on something called the grammar of graphics. By default, ggplot2 takes care of many of the fiddly details that make plotting a hassle when using the plotting functions provided by base R (like drawing legends, and picking good colours). It also provides a powerful framework which makes creating complex graphics easy.9 When you see analyses performed by various data bloggers they will often be using ggplot2 to visualise their data.

To see the many functions this package provides view its top level help-file with

1.5.2 Diamonds data

Let us utilise the functionality of ggplot2 by exploring a data set describing the prices and other attributes of 53,940 diamonds. Make sure your working directory is setup correctly, read the data into R. Check it has loaded properly by comparing the dimensions to what is shown below:

## [1] 53940    10

The ten variables are described in Table 1.5.

Table 1.5: Variable description of the diamonds data set. Ranges of each variable are stated in brackets.
Variable Description
price price in US dollars ($326–$18,823)
carat weight of the diamond (0.2–5.01)
cut quality of the cut (Fair, Good, Very Good, Premium, Ideal)
colour diamond colour, from J (worst) to D (best)
clarity measurement of how clear the diamond is: I1 (worst), SI1, SI2, VS1, VS2, VVS1, VVS2, IF (best)
x length in mm (0–10.74)
y width in mm (0–58.9)
z depth in mm (0–31.8)
depth total depth percentage \(= 2\times z/(x + y)\) (43–79)
table width of top of diamond relative to widest point (43–95)

How the different measurements relate to a diamond are shown in Figure 1.1. With table then being calculated as follows: \[\begin{eqnarray*} \text{depth} &=& \text{z / diameter}\\ \text{table} &=& \text{(width / x) * 100} \end{eqnarray*}\]

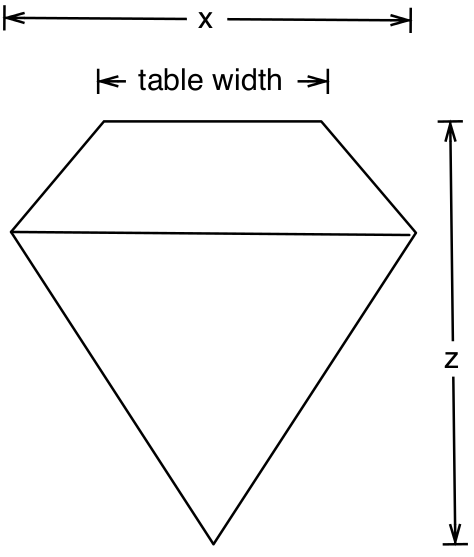
Measuring a diamond.

Figure 1.1: Measuring a diamond.

To check how the data looks type into the R Console:

## # A tibble: 6 x 10
##   carat cut       color clarity depth table price     x     y     z
##   <dbl> <ord>     <ord> <ord>   <dbl> <dbl> <int> <dbl> <dbl> <dbl>
## 1 0.23  Ideal     E     SI2      61.5    55   326  3.95  3.98  2.43
## 2 0.21  Premium   E     SI1      59.8    61   326  3.89  3.84  2.31
## 3 0.23  Good      E     VS1      56.9    65   327  4.05  4.07  2.31
## 4 0.290 Premium   I     VS2      62.4    58   334  4.2   4.23  2.63
## 5 0.31  Good      J     SI2      63.3    58   335  4.34  4.35  2.75
## 6 0.24  Very Good J     VVS2     62.8    57   336  3.94  3.96  2.48
## # A tibble: 6 x 10
##   carat cut       color clarity depth table price     x     y     z
##   <dbl> <ord>     <ord> <ord>   <dbl> <dbl> <int> <dbl> <dbl> <dbl>
## 1  0.72 Premium   D     SI1      62.7    59  2757  5.69  5.73  3.58
## 2  0.72 Ideal     D     SI1      60.8    57  2757  5.75  5.76  3.5 
## 3  0.72 Good      D     SI1      63.1    55  2757  5.69  5.75  3.61
## 4  0.7  Very Good D     SI1      62.8    60  2757  5.66  5.68  3.56
## 5  0.86 Premium   H     SI2      61      58  2757  6.15  6.12  3.74
## 6  0.75 Ideal     D     SI2      62.2    55  2757  5.83  5.87  3.64

Make sure that the levels for each of the factors are in the correct order, because, by default, R will simply order the levels alphabetically.

## [1] "Fair"      "Good"      "Very Good" "Premium"   "Ideal"

To fix this, apply the factor() function, but with the levels in the correct order:

Check the other factors, and correct them if necessary.

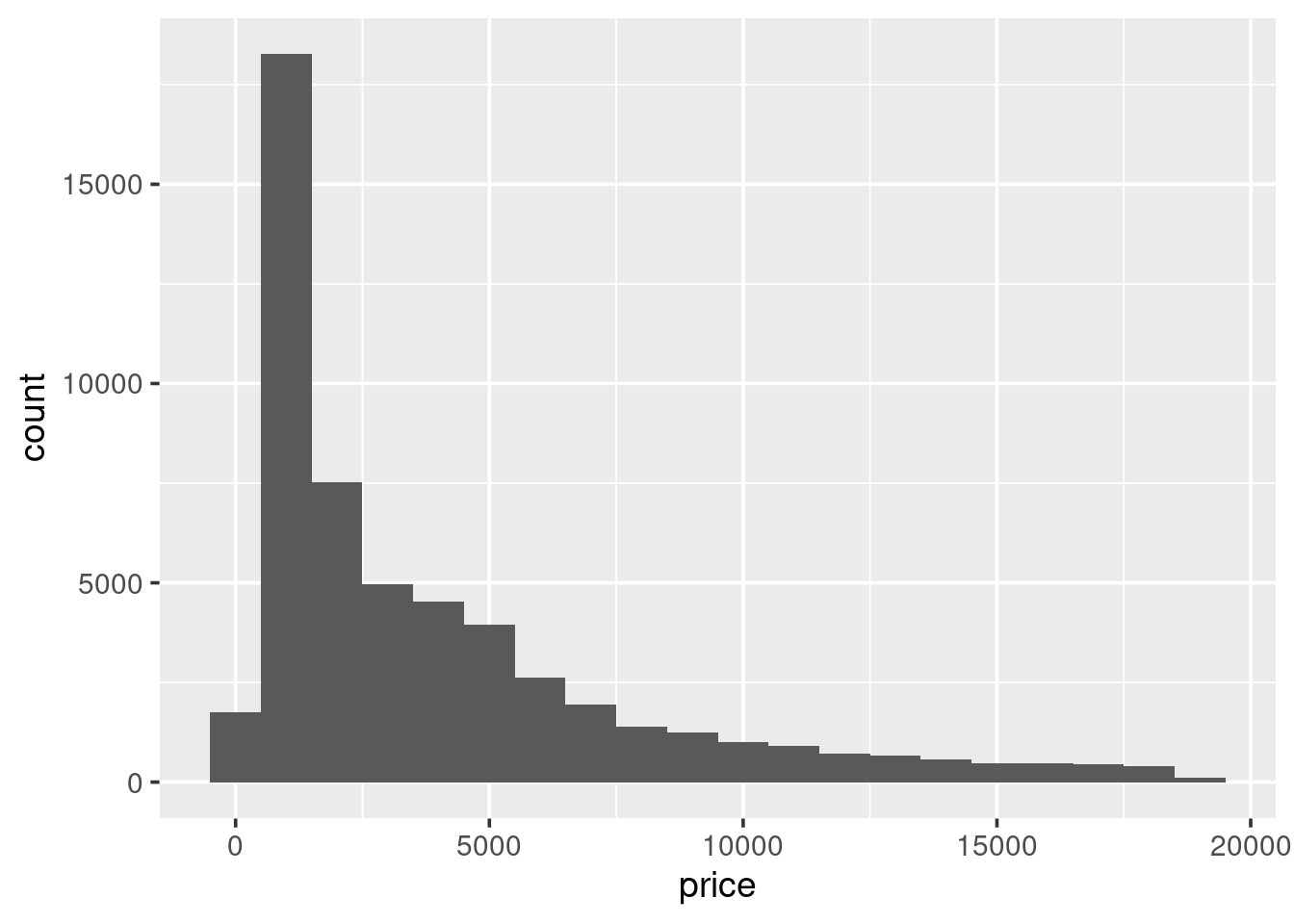
1.5.3 Histograms

A histogram shows the distribution of a single numeric variable, by showing us the frequency with which certain intervals of the data occur. Use qplot() to produce a histogram of the carat distribution:

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.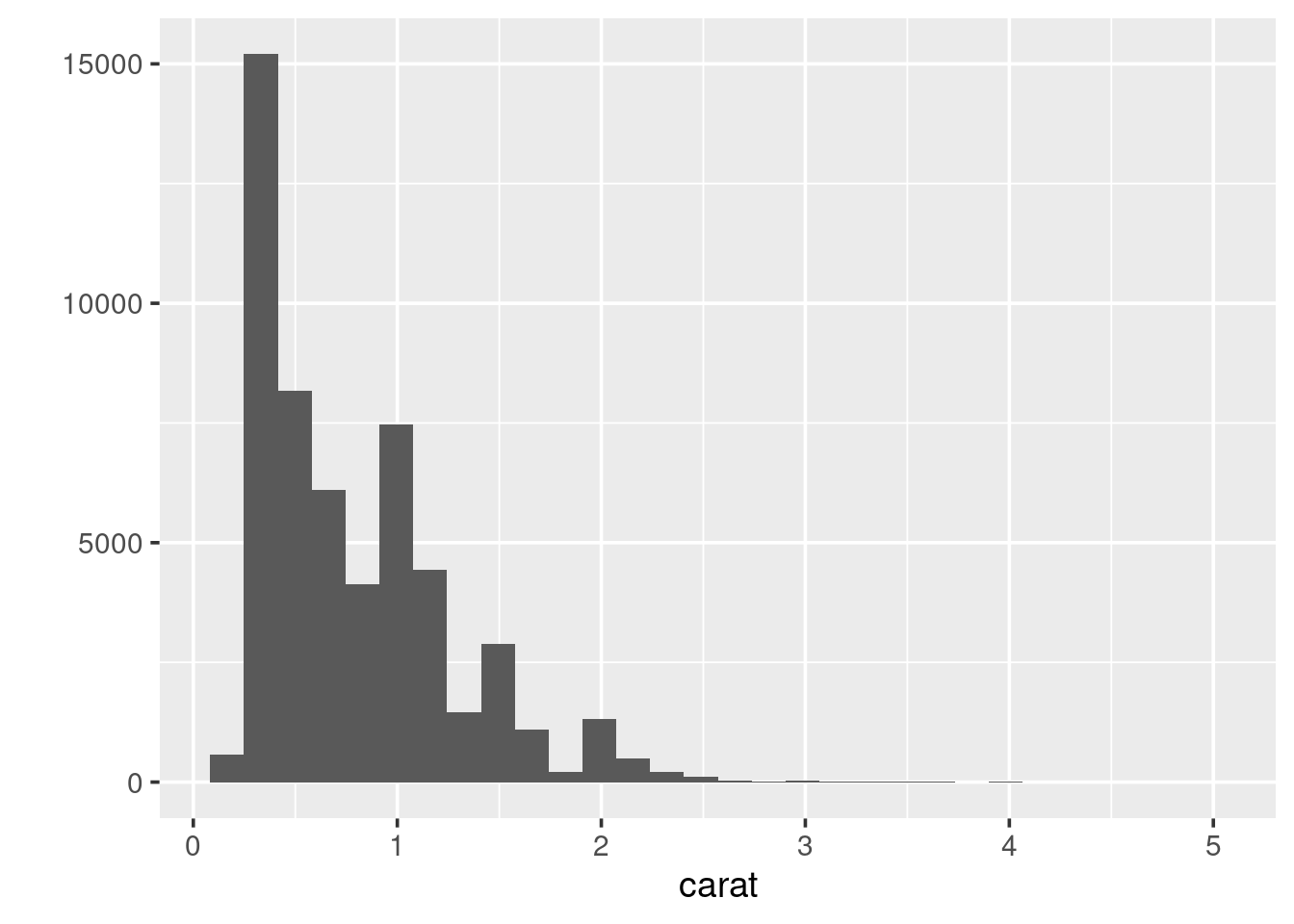

Because the data is strictly continuous, it needs to be binned. By default ggplot2 splits the data up into 30 equally-sized intervals (bins). To alter this:

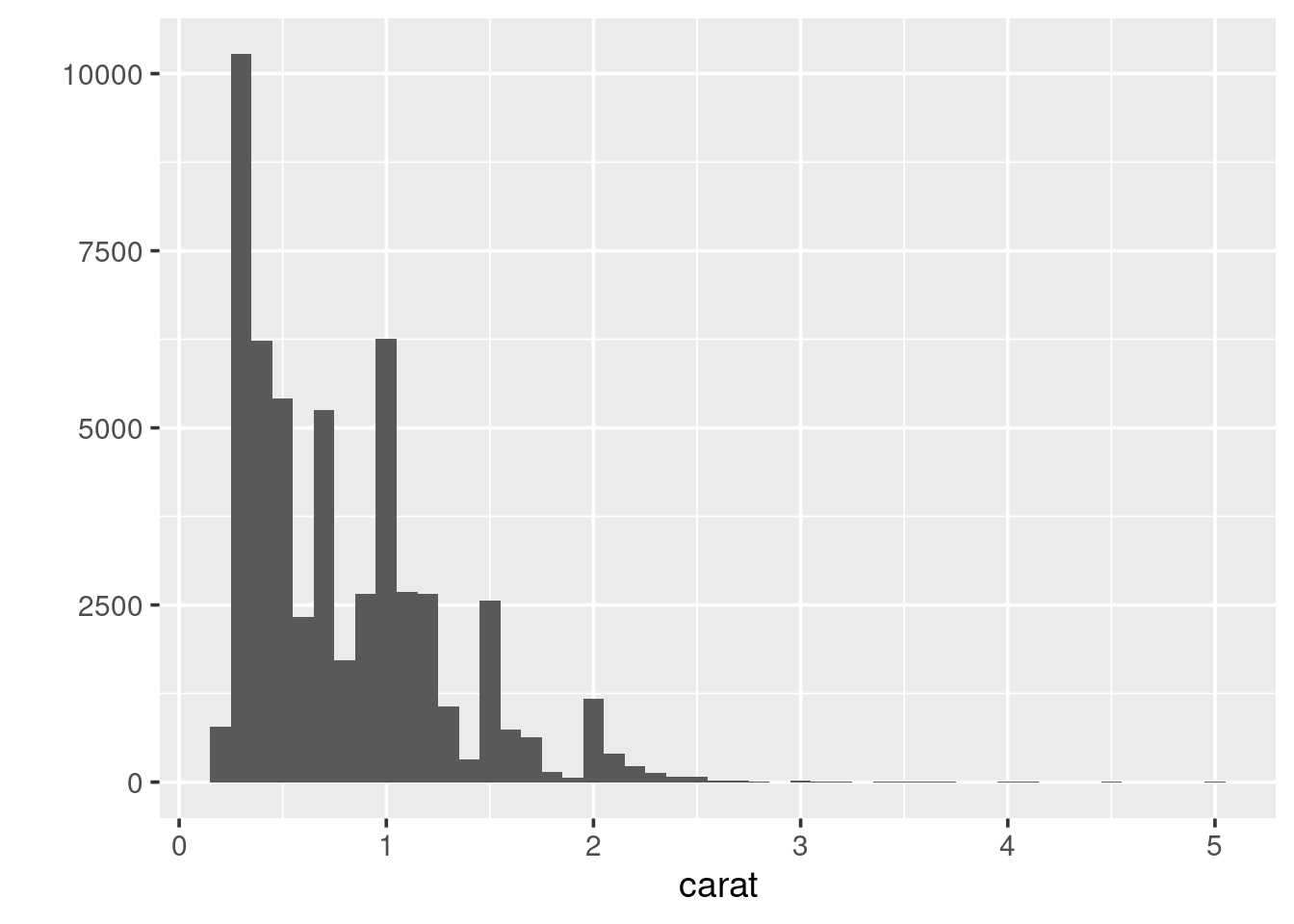
Always experiment with the bin width. Try increasing it slowly up to 1. Pay attention to how features in the data become smoothed out?

This histogram shows the carat distribution for all of our data. But does this general shape hold if we look at different categories of diamond? For example, does the carat distribution change depending on the cut. The easiest way to do this is to, graphically, reproduce the histogram for each type of cut. This process is called faceting. To create a faceted plot using the cut variable modify the previous code so it now looks like the following and run it:

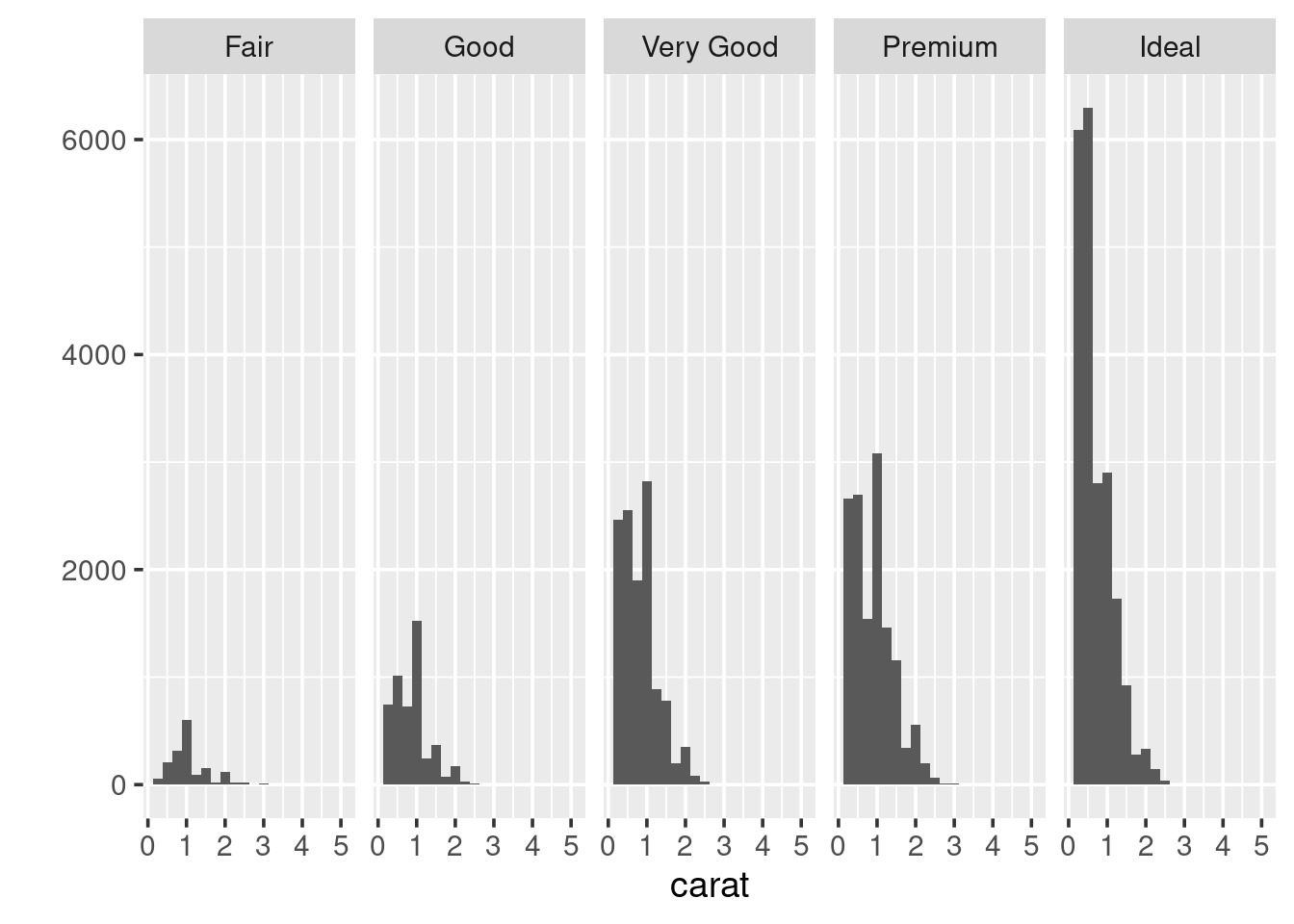
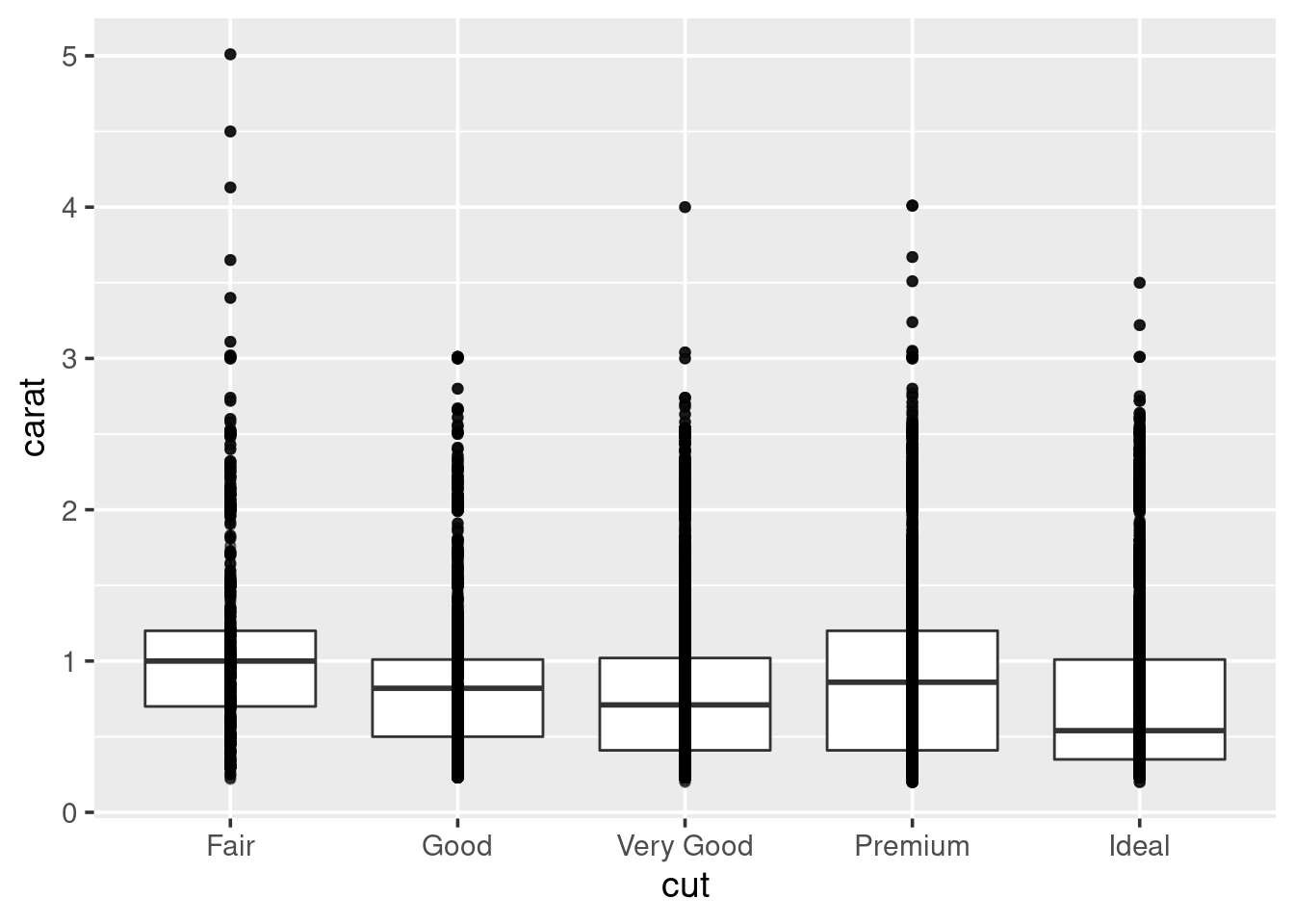
So, it looks like the distribution stays fairly similar across each of the cut types. But it is hard to really say with any confidence, because the number of diamonds with a particular cut varies, considerably. It may be more useful to look at boxplots.

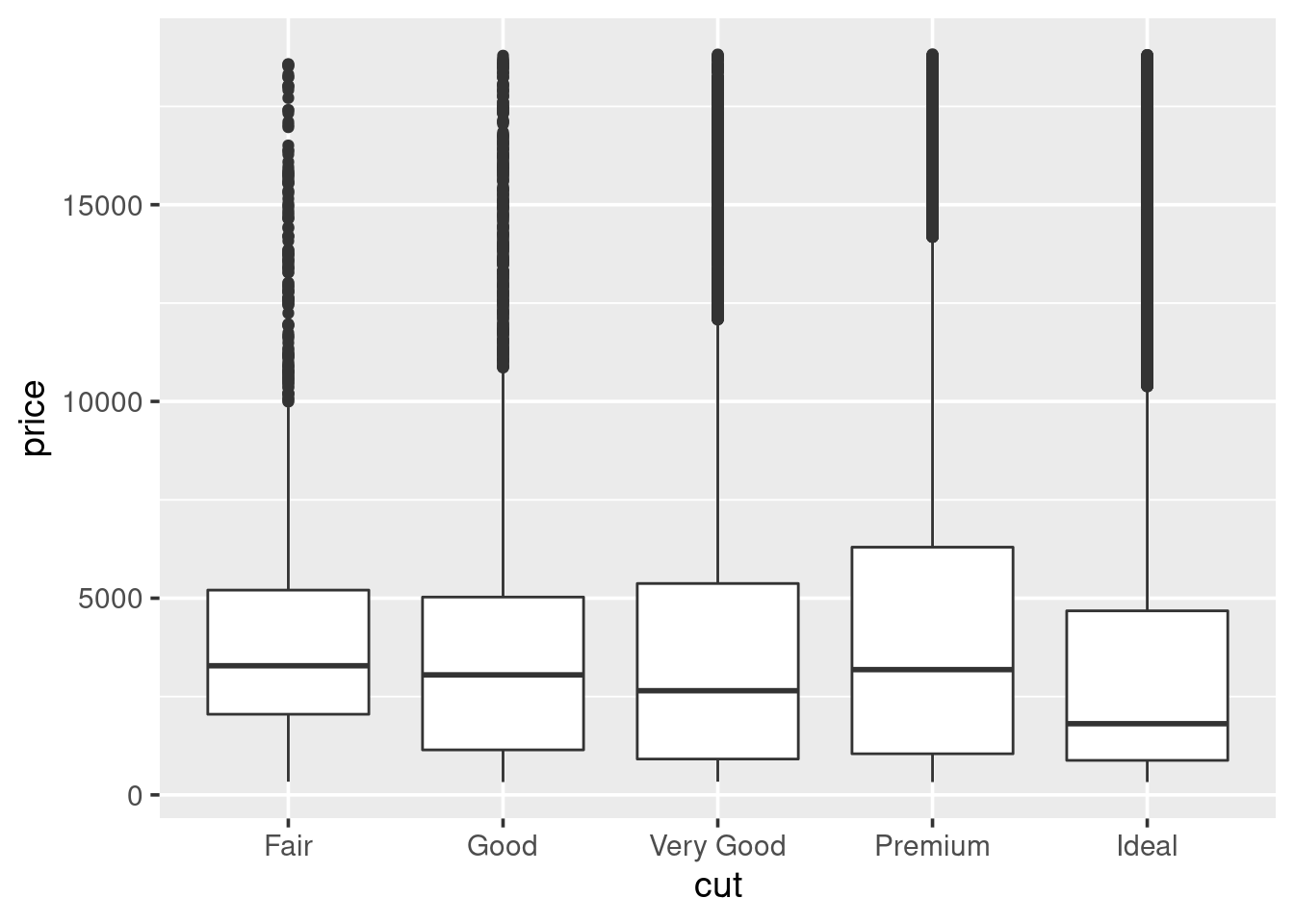
1.5.4 Boxplots

A boxplot (sometimes called a box-and-whisker plot) is an alternative to producing a histogram, when we want to look at the distribution of a variable but for different categories of another variable. For example, the carat distribution (continuous) with each of the different cut types (categorical).

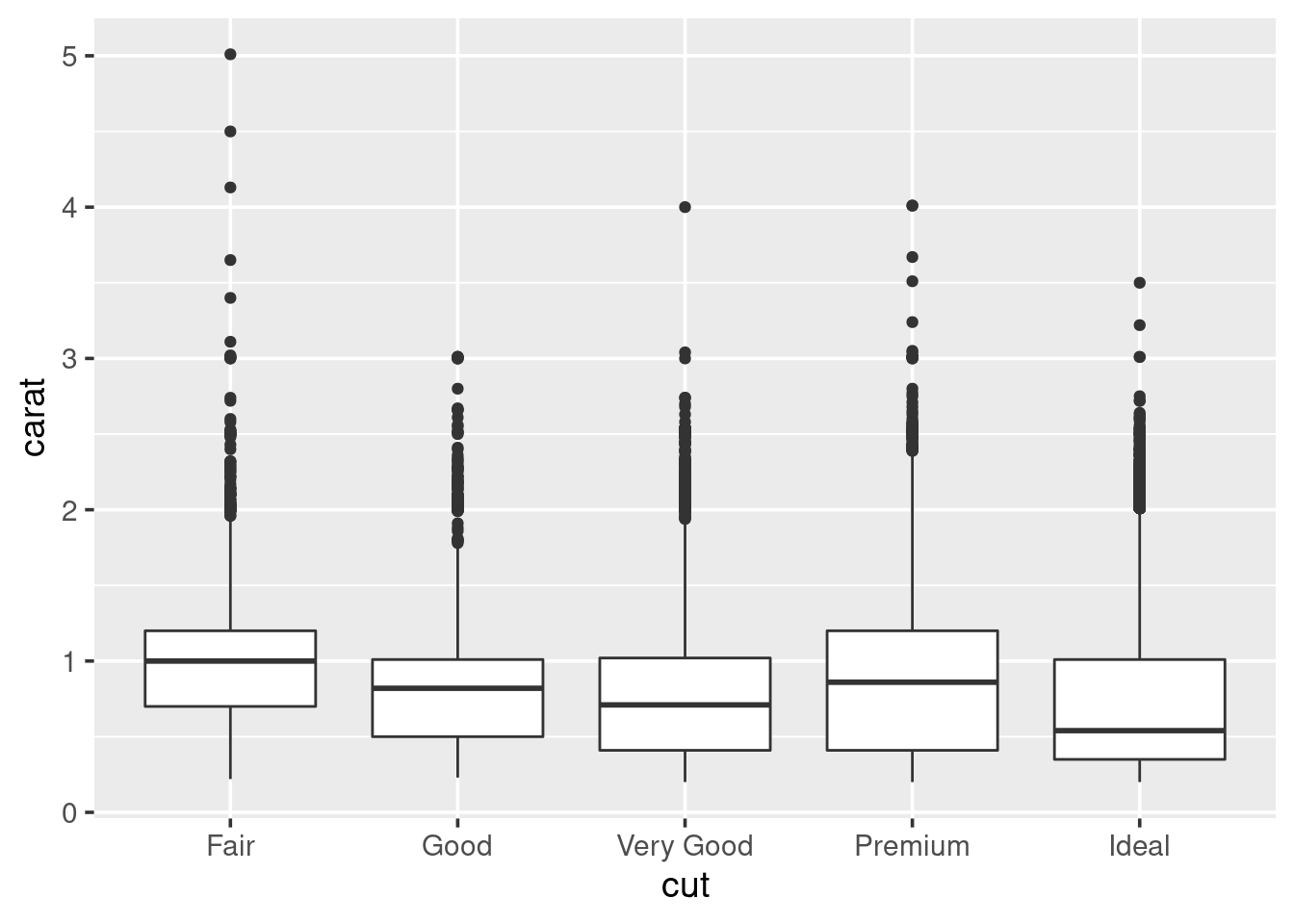
Each set of box and whiskers relies on five numbers to summarise the carat distribution for each particular cut. The middle three values are the 25%, 50% and 75% quantiles. To calculate these we simply order the data from lowest to highest, and then lookup the values that are 25%, 50% and 75% along the vector. The 50% value is more commonly know as the median, while the 25% and 75% are referred to as lower and upper quartiles (Q1 and Q3 respectively) because they are a quarter into the data range, from either end.

## [1] 0.7
## [1] 0.7

Similarly for the quantiles:

## [1] 0.40 1.04
##  25%  75% 
## 0.40 1.04

The two quartiles are then used to draw the main box, with the median being the solid line inside the box. How are the whiskers calculated, and what are the other points? The other points are considered outliers, this means that they are thought to deviate too far from the rest of the data to be considered a part of the main distribution.

How we identify if something is an outlier is related to the length of the whiskers. The whiskers stem from the main box up and stop at either the range of the data or if they hit the following limits:

  • the lower whisker stops at the Q1 - 1.5\(\times\)IQR
  • the upper whisker stops at the Q3 + 1.5\(\times\)IQR

Where IQR represents the Inter-Quartile Range; IQR = Q3 - Q1, also know as the length of the box. Due to the definitions of Q1 and Q3, the box represents 50% of the data.

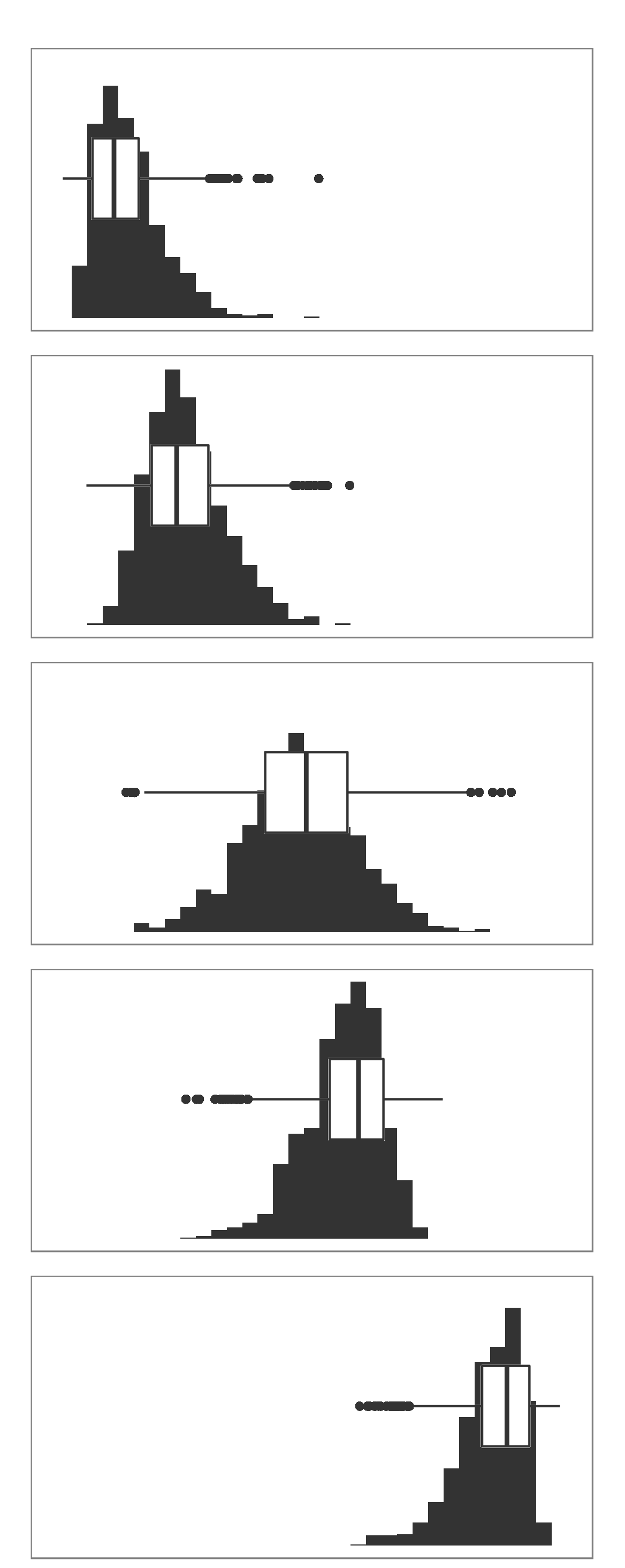
Finally, because boxplots and histograms are effectively trying to summarise the same data, therefore patterns in one correspond to patterns in another, as shown in the margin.

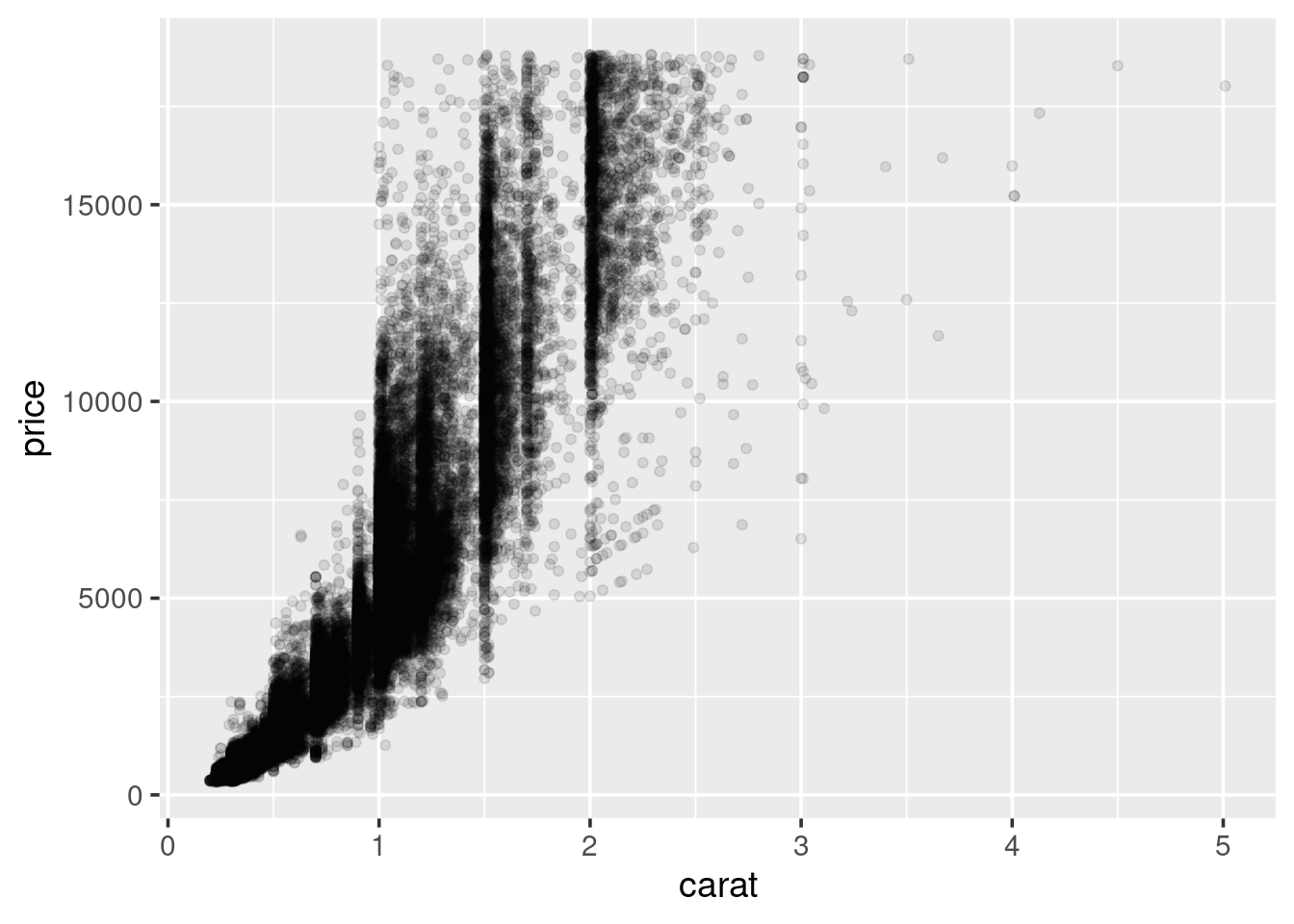
1.5.5 Scatter plots

A scatter plot can be used when both variables of interest are numeric (continuous). A scatter plot contains a point for each observation in the data. We can use scatter plots to explore the relationship between the price of the diamond and the other attributes. Start with carat:

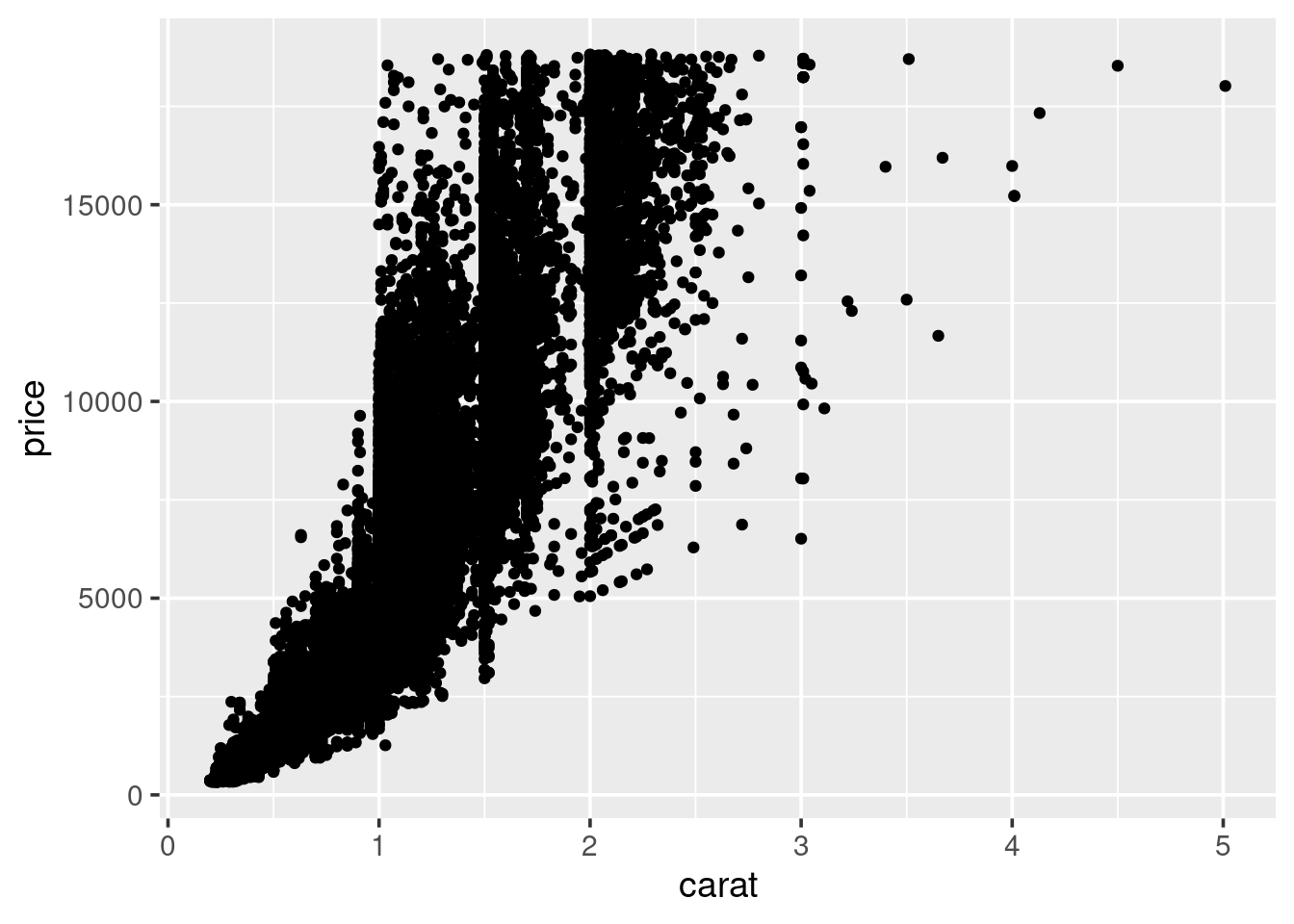
So, we see a general positive relationship between the weight of the diamond (carat) and it’s price. It might be reasonable to assume that it’s price is also related to it’s cut.

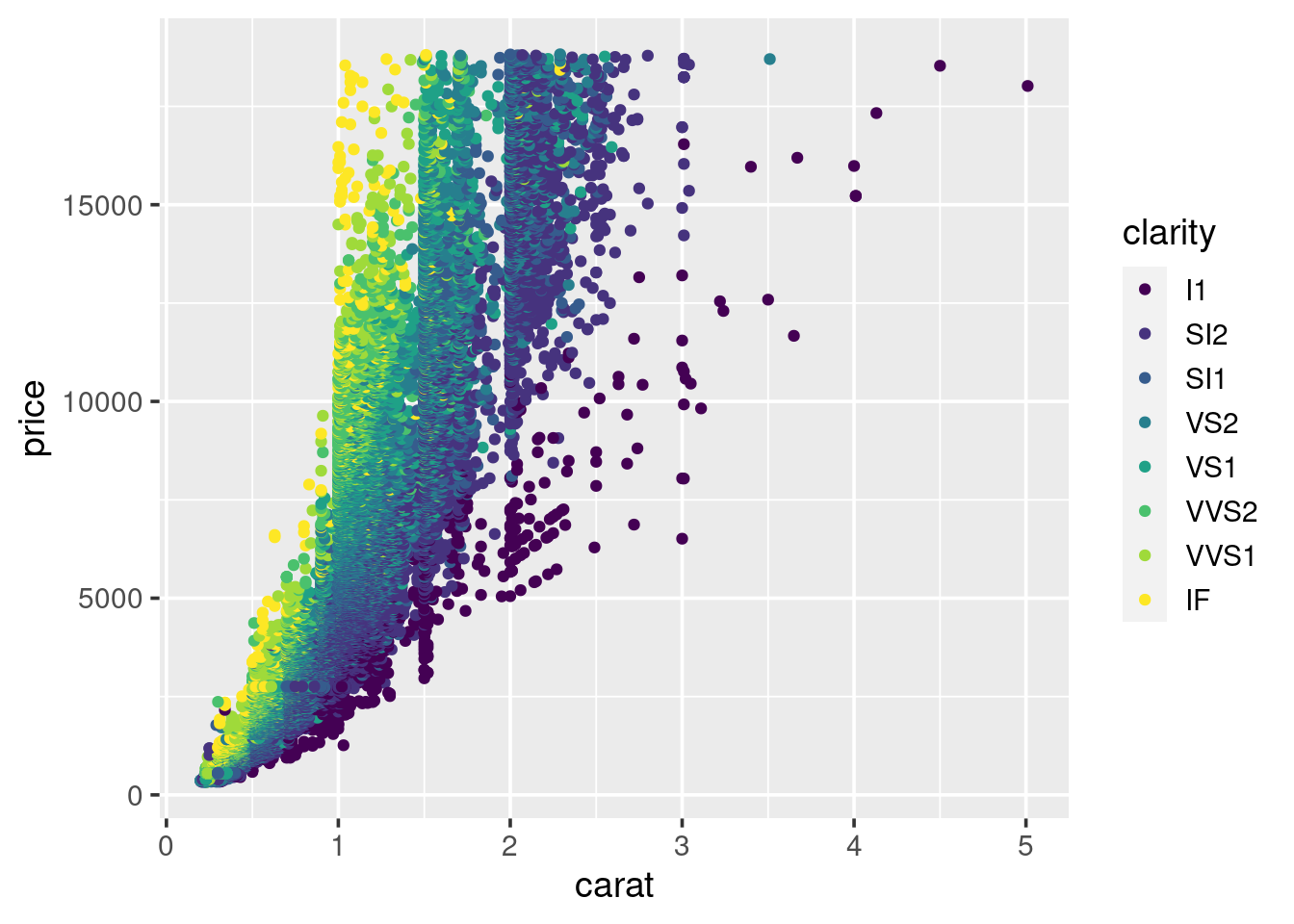
We can see some separation according to colour. This may be improved by faceting the plot by clarity, similar to what we did for the histograms. Try doing this now.

1.5.6 Bar charts

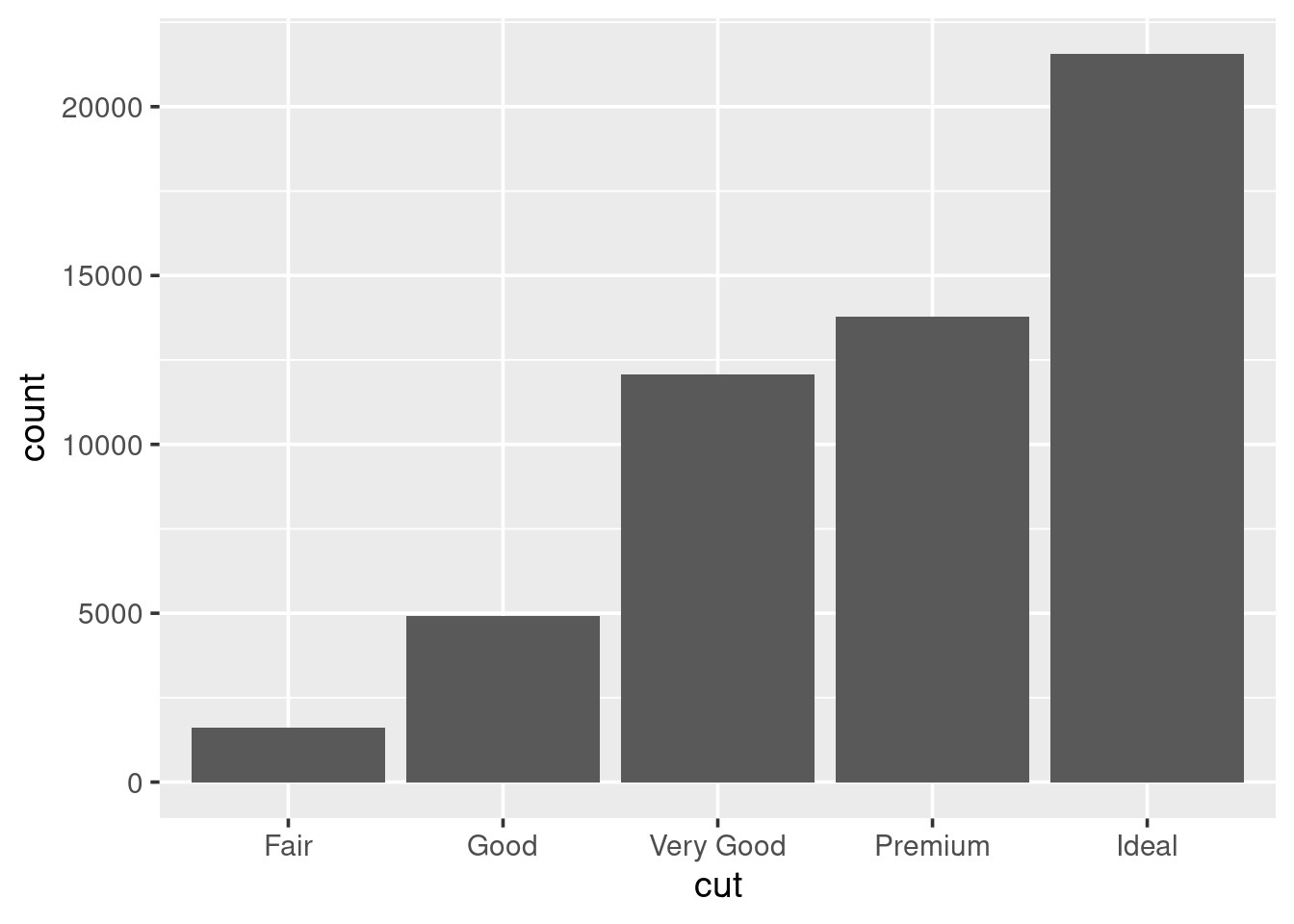
When wanting to look at the distribution of a categorical variable we use a bar chart:

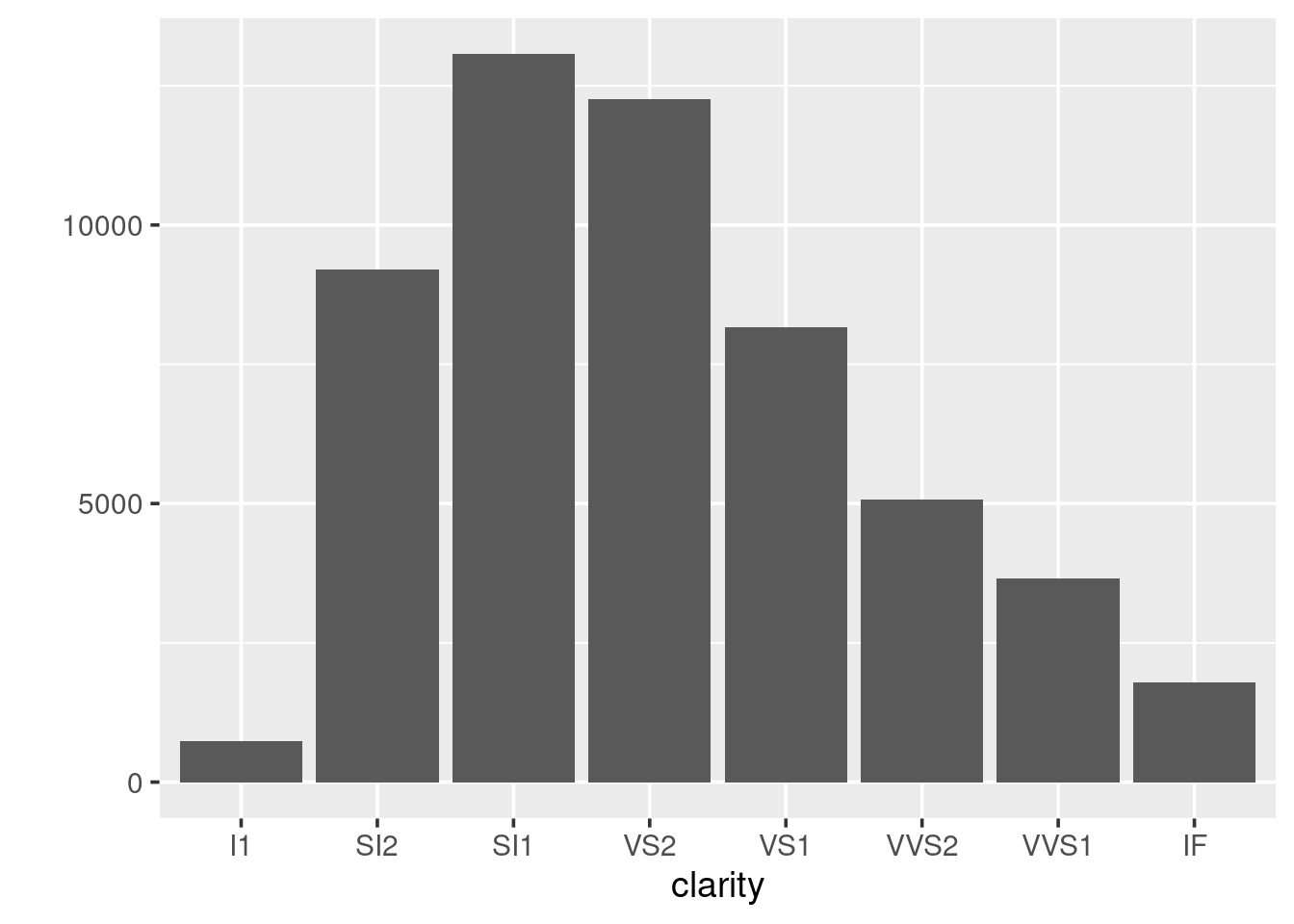
We can fill in the bars with colour according to the cut:

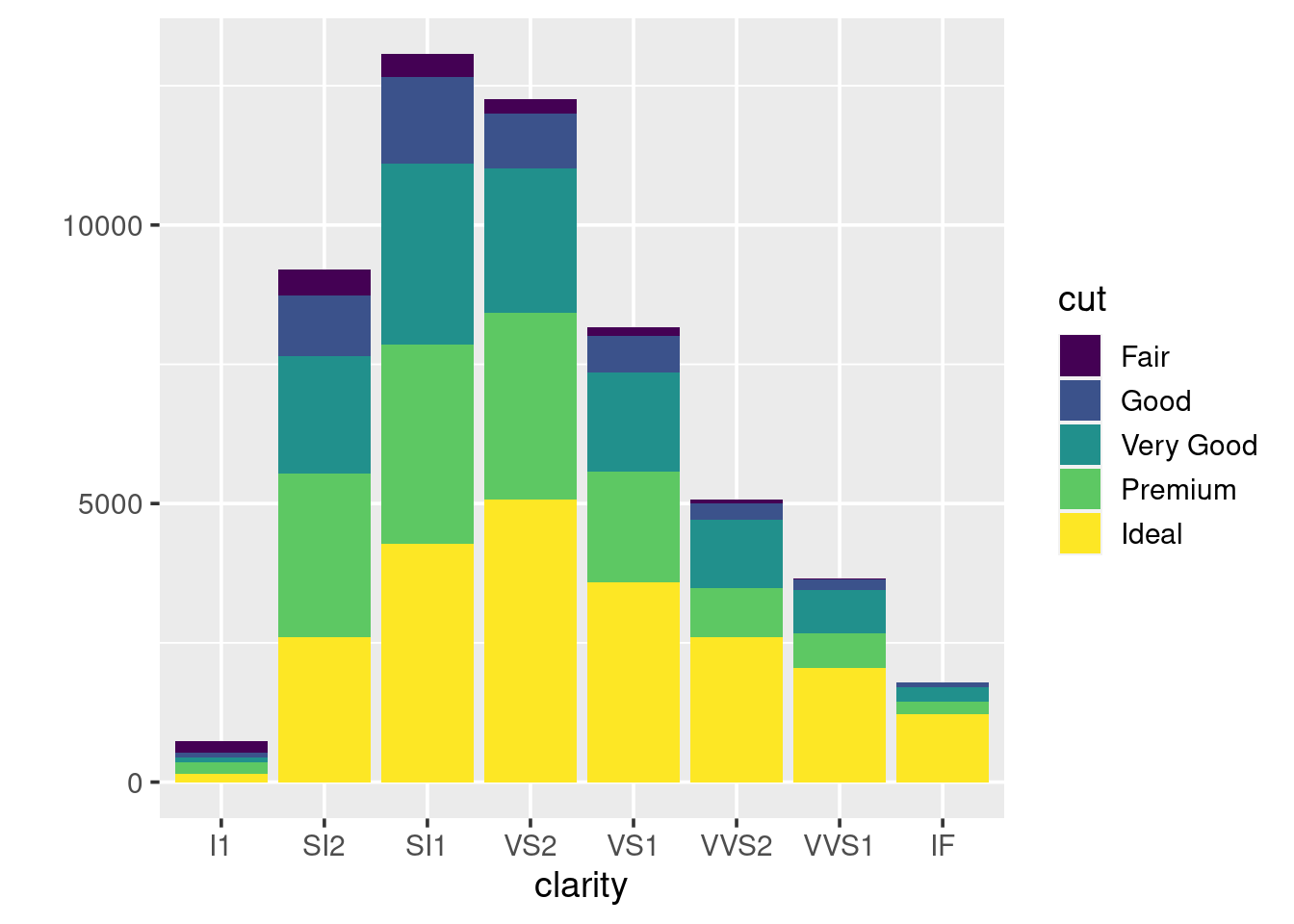
What happens if you set the colour argument to be equal to cut, instead of using fill?

1.5.7 How to save plots

There is no point in making pretty graphs if you cannot include them in a report or blog post. To save your amazing art work, first you need to store the plot in an object:

Because we are now storing the plot inside an object, R no longer automatically prints it to the screen. Simply enter the object name in the console to see it.

To save the plot to a file, we pass the object to theggsave() function:

The width and height are automatically assumed to be specified in inches. If you prefer to use mm or cm then set the units argument according. Check the help page for other arguments.

When saving plots to include in a report, the maximum you should be setting your width to is about 6 inches (15cm), so that it does not extend beyond the margins on an A4 page.

After saving the clarity bar plot, try importing it into a Word document. If it looks too big, do not resize it in Word, instead alter the values used by ggsave(). This way, after a bit of tweaking, you will have a script that produces the exact graph you want to use.

1.5.8 Going deeper with ggplot

We have been making heavy use of the qplot() function, but we need to go deeper. In order to modify other parts of the graph such as axis labels, the number of tick marks, and the colouring scheme that is used, we need to become pro-ggplotters. To become pro we need to stop using qplot() and start using it’s big sister ggplot().

First we will recreate some of the graphs we have already seen, so that you spot the subtle differences in code. To produce the scatter plot of carat vs price:

For boxplots of carat vs cut:

By using ggplot() we are now starting to use the layering approach to making graphics. The only thing we give ggplot() is the data frame. Next we start to add-on our “geom”s, these are the different shapes and summaries that can be plotted.

Here are some of the geoms available in ggplot2, a full list is at http://docs.ggplot2.org :

  • geom_abline
  • geom_area
  • geom_bar
  • geom_bin2d
  • geom_boxplot
  • geom_contour
  • geom_density
  • geom_density2d
  • geom_dotplot
  • geom_hex
  • geom_histogram
  • geom_hline
  • geom_jitter
  • geom_line
  • geom_point
  • geom_rug
  • geom_smooth
  • geom_text
  • geom_violin
  • geom_vline

In order to use a geom we need to map our variables to the different aesthetics it uses. Aesthetics of a geom include; position on the x-axis and y-axis, colour, size, transparency, and more. We map our variables to the aesthetics through the aes() function within the particular geom_*().

In order to look at cut vs clarity, we previously drew a boxplot. We can take this further by overlaying points on top of the boxplots:

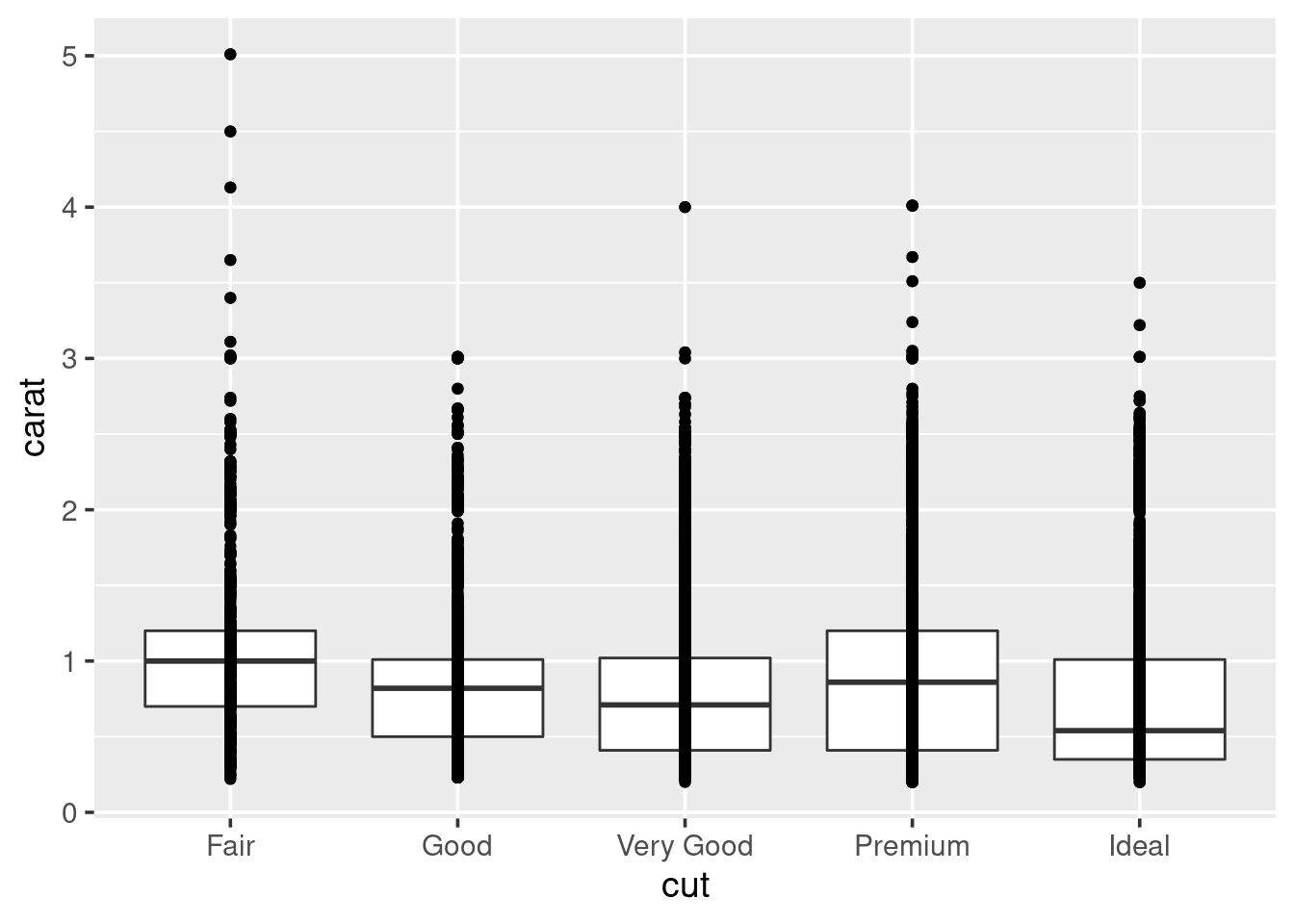
This does not look pretty. In fact, there is probably a lot of overplotting going on, to improve this try swapping out geom_point for geom_jitter and rerunning the plot. What does it look like now?

Well, now we can not see the boxplots. Try making the points semi-transparent by setting their alpha transparency level to be small:

“Alpha” in graphics refers to how transparent something is, usually pixels. Alpha values can range between \(1\) (solid) to \(0\) (invisible). By playing with the alpha value you can begin to get an impression of how stacked the data is. Try lowering it till you can start to see some of the shapes in the data.

I do not think we are ever going to be able to see the boxplots below the points, so go ahead and swap the lines of code for each geom around, and rerun the plot.

Within the boxplots, we can turn off the fill of the boxes by setting fill=NA, and turn the colour of the lines used for the boxes and whiskers to white:

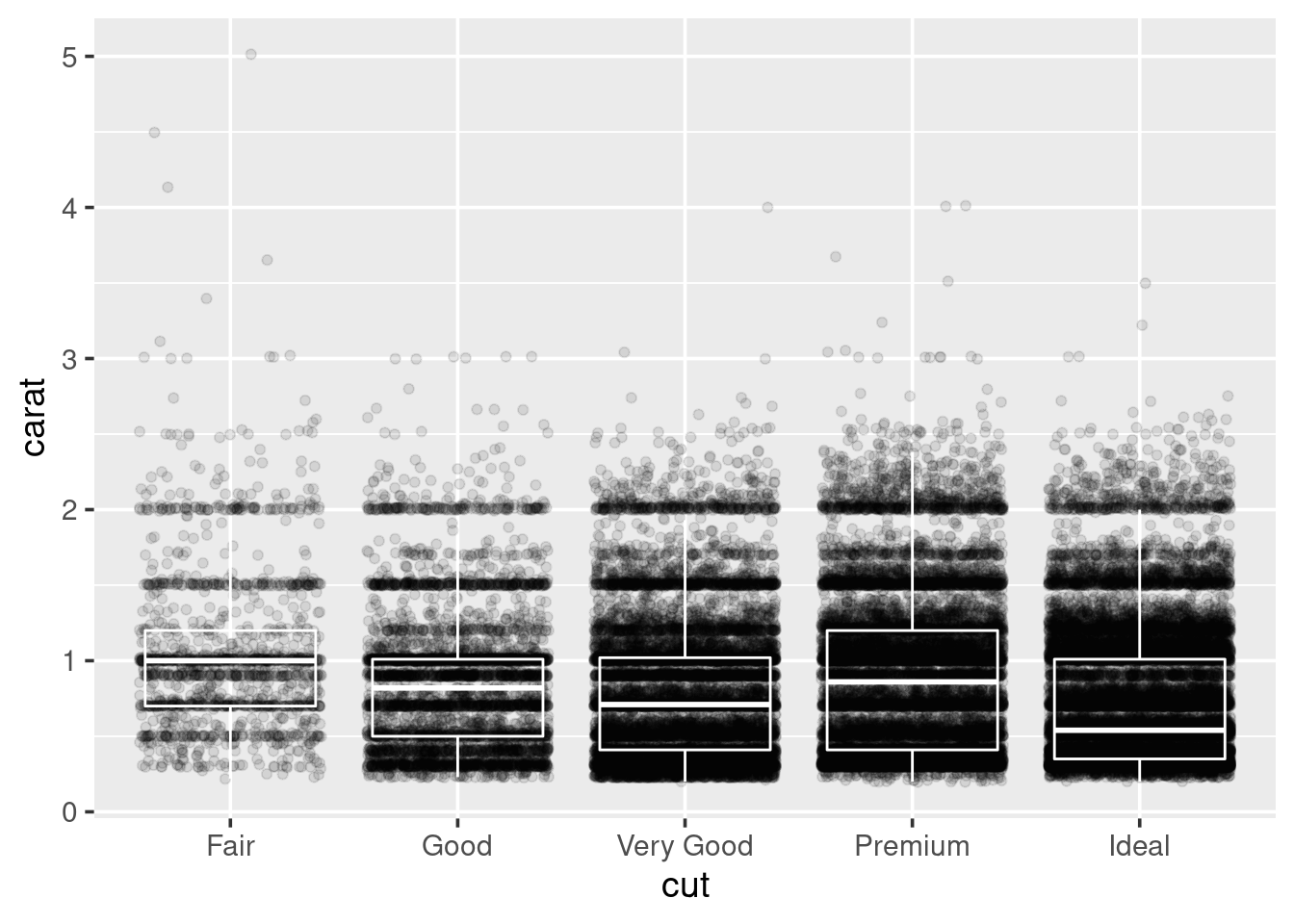
Look-up the help page for labs, and use it to rewrite the axis labels so that they start with capital letters. Also, look up the help page for theme_bw, and see how to add this to your plot.

To save this to a file, do what you did before; store it to an object and use ggsave():

1.5.9 Summary

  • The base environment in R provides plotting functions such as plot(), hist(), and many others. But these plotting functions often have inconsistent arguments, nor do they make it easy to customise the graphs that are produced, nor do they frequently have sensible defaults for things like legends or colours. The ggplot2 package attempts to alleviate these problems by providing a layered system to creating graphics.

  • An example of a scatter plot:

  • An example of a barchart:

  • An example of a histogram:

  • An example of a boxplot:

  • Aesthetics of a geom generally include: x; y; size; colour; fill; shape; group; alpha. But there are others for specific geoms, check the help pages or online documentation for more information.

  • When producing graphics for a printed report (like on actual physical A4 paper), then append theme_bw(base_size=10) as an extra function to your ggplot command. This will switch the formatting of the plot so it is less ink-intensive and also change the font size to be 10pt.

  • Use the ggsave() function to save the plot as a PNG file, width and height are specified in inches by default:

  • Documentation is at http://docs.ggplot2.org and there have been many ggplot2 questions answered on StackOverflow.

1.5.10 Exercises

  1. Explore the diamonds data set some more. In particular, look at how the different attributes relate to price. Try to visualise several different attributes at once in relation to price, by mapping different variables to several of the available aesthetics.

Hint: check the “Aesthetics” section of the help page for each geom to see what aesthetics can have variables assigned to them.

  1. Once you have identified a plot you like the look of make sure that you have a script you can run with source which will save this plot to a file.

  2. Download the titanic.csv file from the module page on moodle. This data set provides information on the fate of passengers on the fatal maiden voyage of the ocean liner Titanic. The data set contains information on whether or not the passengers survived, along with information on economic status (class), sex, and age, see Table 1.6.

Table 1.6: Variable description of the Titanic data set.
Variable Levels
class 1st, 2nd, 3rd, Crew
sex m, f
age child, adult
survived no, yes

  1. The plan is to explore this data set using graphs. So, start a new script, and add your packages to the top along with an initial comment.

  2. Write your code to read in the data set, and make sure the data is actually read in correctly.

  3. Rewrite the levels for sex, so we have male and female' instead ofmandf`, respectively.

  4. First, draw a bar chart showing the number of those that did anddid not survive. Save this to a file.

  5. Now consider, separately, how class, sex and age relate to whether or not someone survived. Make comments in your script about any observations you make.

Tip: You can change the way your bar charts look by altering the position argument within geom_bar(), by default it is set to position="stack", alternatives include "fill" and "dodge": geom_bar(..., position="dodge")

  1. How might you change the bar charts so instead of looking at counts you are looking at percentages? (You will need to research this). For example, rather than looking at how many males vs females died, we would like to see what percentage of males survived, vs what percentage of females.

Once you have this working, reconsider class, sex, and age.

  1. Look at two attributes at once with survived.

  2. How would you produce plots that only consider the relationships between class, sex, age for passengers, and ignore crew? Do this.

  1. FYI read.csv() is just a wrapper for the heavy-lifter that is read.table(), but changes the defaults to suit CSV files. R developers think of everything!↩

  2. If you are not familiar with the term directory, we just mean folder. Technically speaking there is a difference between a directory and a folder.↩

  3. The only name for this object I could think of was planet_earths which I think is ugly, see if you can do better.↩

  4. I should say easier than normal.↩